Question

What is the area of a rectangle with vertices (-8-2) (-3-2) (-3-6) (-8-6)

Answer 1

Answer: The area of the given rectangle is 20 sq. units.

Step-by-step explanation: We are given to find the area of a rectangle with the co-ordinates of the vertices as (-8-2), (-3-2), (-3-6) and (-8-6).

Let the co-ordinates of vertices of the given rectangle be A(-8-2), B(-3-2), C(-3-6) and D(-8-6).

Then, the lengths of the sides AB, BC, CD and DA are calculated using distance formula as follows:

`AB=√((-3+8)^2+(-2+2)^2)=√(25)=5~\textup{units},\\\\BC=√((-3+3)^2+(-6+2)^2)=√(16)=4~\textup{units},\\\\CD=√((-8+3)^2+(-6+6)^2)=√(25)=5~\textup{units},\\\\DA=√((-8+8)^2+(-2+6)^2)=√(16)=4~\textup{units}.`

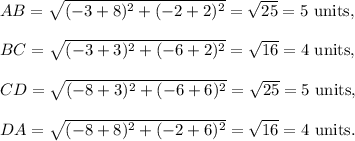
So, the length of the rectangle is 5 units and its breadth is 4 units.

We know that the area of a rectangle is the product of its length and breadth, so the area of the given rectangle will be

`A=5*4=20~\textup{sq units.}`

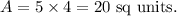
Thus, the area of the given rectangle is 20 sq. units.

Answer 2

See the attached picture: