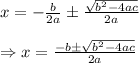Question

Derive the quadratic formula. Drag and drop the correct expression to complete the derivation of the formula. I'm having a little trouble remembering the steps.

Answer 1

The derivation of the quadratic formula is done using completing the square as shown below.

Given a quadratic equation:
`a x^(2) +bx+c=0`.

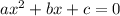
Make the coefficient of
`x^2` to be 1 by dividing through by a, to get
`x^2+ (b)/(a) x+ (c)/(a) =0`.

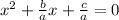
Next, take the constant term (the term with no x) to the other side of the equation to get
`x^(2) + (b)/(a) x=- (c)/(a)`.

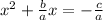
Then add to both sides of the equation, the square of half the coefficient of x, to get:


`x^(2) + (b)/(a) x+\left( (1)/(2)\cdot (b)/(a) \right)^2=- (c)/(a) +\left( (1)/(2)\cdot (b)/(a) \right)^2 \\ \\ \Rightarrow x^2+ (b)/(a) x+ (b^2)/(4a^2) =- (c)/(a) +(b^2)/(4a^2)`

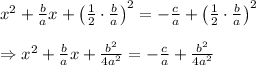
Next, we factorize the left hand side to get
`\left(x+ (b)/(2a) \right)^2 =- (c)/(a) +(b^2)/(4a^2)`.

Then, we take the square root of both sides to get:


`\sqrt{\left(x+ (b)/(2a) \right)^2} =\sqrt{- (c)/(a) +(b^2)/(4a^2)} \\ \\ \Rightarrow x+ (b)/(2a)=\pm\sqrt{ (b^2-4ac)/(4a^2) }=\pm ( √(b^2-4ac ))/(2a)`

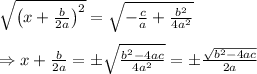
Finally, solve for x, to get:


`x=- (b)/(2a)\pm ( √(b^2-4ac ))/(2a) \\ \\ \Rightarrow x= (-b\pm√(b^2-4ac))/(2a)`