Answer:
8 blocks and 27 blocks.
Explanation:
A cube has a side length of
 inch.
inch.
(A) Let B block with a side length of
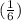 inch will be required to fill the cube.
inch will be required to fill the cube.
so volume of cube = volume of block B
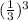 = B ×
= B ×
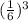
B =
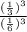
=

=
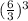
= (2)³ = 8 blocks
(B) Let C blocks with a side length of
 inch will be required to fill the cube.
inch will be required to fill the cube.
Volume of cube = total volume of blocks C
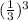 =
=
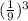 × C
× C
C =
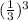 /
/
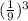
=
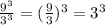
= 27 blocks
Therefore, answer is 8 blocks and 27 blocks.