Question

A plane travels 236 miles in 1. 4 hours against the wind. On the return trip, it travels the same 236 miles in 1 hour. Find the speed of the wind. (Round answer to the tenth)

Answer 1

The first thing we must do for this case is to define variables:
v1: speed of the plane
v2: wind speed
We then have the following system of equations:
With the wind against:
v1 - v2 = 236 / 1.4
Wind in favor:
v1 + v2 = 236/1
Solving the system we have:
v1 = 202.286
v2 = 33.71
Answer:
the speed of the wind is:
v2 = 33.7 miles / hour

Answer 2

Speed is given by the distance traveled divided by the time spent.

The net speed with which the plane traveled against the wind is given by
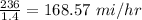
`(236)/(1.4) =168.57\ mi/hr` while the speed with which the plane travelled in the return trip is given by
`(236)/(1) =236\ mi/hr`

Let the speed of the plane be v and the speed of the wind be w, then when the plane was traveling against the sun, we have, v - w = 168.57 and when the plane is travelling in the direction of the wind, we have, v + w = 236.

Subtracting the first equation from the second equation, we have: 2w = 236 - 168.57 = 67.43

Thus, w = 67.43 / 2 = 33.715

Therefore, the speed of the wind is approximately 33.7 mi/hr.