Answer:
The correct option is D.
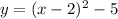
Explanation:
If the vertex V of the parabola has the following coordinates :
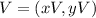
One way to write the equation of the parabola is :
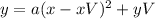
Where xV and yV are the coordinates from the vertex of the parabola and ''a'' is a real number.
If
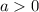 ⇒ The parabola is concave upward
⇒ The parabola is concave upward
If
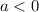 ⇒ The parabola is concave downward
⇒ The parabola is concave downward
In this exercise
 ⇒
⇒
One way to write this parabola is
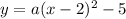
The graph of the parabola is concave upward ⇒
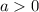
The option D. is
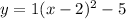 Where
Where
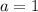 and
and
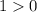 ⇒
⇒
The correct option is D.