Question

How many distinct arrangements of four letters (without repeats) from the set {a, b, c, d, e} are possible? 15?

Answer 1

From the pool of 5 letters, we're picking 4. We can arrange the 4 we picked in
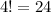
`4!=24` ways.

But there are 5 ways of *not* picking the remaining letter. To account for the arrangements containing the letter not picked, we multiply this total by 5.

Put another way, suppose we drew a, b, c, and d, but not e. We have 24 possible arrangements for these 4 letters, but for any distinct arrangement there are 5 ways of replacing any letter with e.

So the number of arrangements we can actually make is
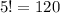
`5!=120`.