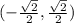Question

If north is the direction of the positive y-axis and east is the direction of the positive x-axis, give the unit vector pointing northwest.

Answer 1

A vector pointing northwest passes through point (-1, 1).

Thus an example of a unit vector pointing northwest is
`-i+j`.

Recall that a vector is made a unit vector by dividing each component of the vector by the magnitude of the vector.

The magnitude of vector
`-i+j` is given by
`|-i+j|=√((-1)^2+1^2)=√(1+1)}=√(2)`.

Thus, a unit vector pointing northwest is
`- (1)/(√(2)) i+ (1)/(√(2)) j` which when we rationalize we have
`- (√(2))/(2) i+ (√(2))/(2) j`.

Answer 2

North is the direction of positive y-axis. East is the direction of positive x-axis. So West will be the direction of negative x-axis.

Northwest will mean, in between north and west i.e. in between y-axis and the negative x-axis which is the mid of the 2nd quadrant. Thus the vector pointing northwest will form an angle of 135 degrees with positive x-axis.

The magnitude of unit vector is 1 and is forming an angle of 135 degrees. In terms of its components, we can write:

x-component = 1 cos (135) =
`- ( √(2) )/(2)`
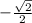
y-component = 1 sin (135) =
`( √(2) )/(2)`

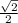
Thus the unit vector will be =
`- ( √(2) )/(2)x+ ( √(2) )/(2)y`

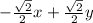
In vector form, component form the vector can be written as:


`(- ( √(2) )/(2), ( √(2) )/(2))`