Question

Find all local extrema for f(x, y) = 4y3 + 18x2 − 36xy. (if an answer does not exist, enter dne.)

Answer 1

The local extremas of a function, f(x), occur when the derivative of the function, f'(x), equals zero.

Given the function:
`f(x, y) = 4y^3 + 18x^2 - 36xy`

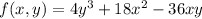
The derivative of the function is given by:


`12y^2f'(x)+36x-36[xf'(x)+y]=0 \\ \\ \Rightarrow12y^2f'(x)+36x-36xf'(x)-36y=0 \\ \\ \Rightarrow(12y^2-36x)f'(x)=36y-36x \\ \\ \Rightarrow f'(x)= (36(y-x))/(12(y^2-3x)) = (3(y-x))/(y^2-3x)`

At the local extremas,
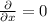
`(\partial)/(\partial x) =0` and
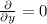
`(\partial)/(\partial y) =0`. i.e.
`(\partial)/(\partial x) =(\partial)/(\partial y)`

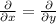
Recall that


`f'(x)= ( (\partial)/(\partial x) )/((\partial)/(\partial y)) = (3(y-x))/(y^2-3x) \\ \\ \Rightarrow(\partial)/(\partial x)=3(y-x)\ and\ (\partial)/(\partial y)=y^2-3x`


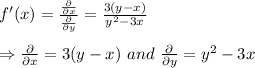
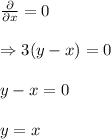
`(\partial)/(\partial x)=0 \\ \\ \Rightarrow3(y-x)=0 \\ \\ y-x=0 \\ \\ y=x` . . . (1)


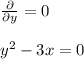
`(\partial)/(\partial y)=0 \\ \\ y^2-3x=0` . . . (2)

But from (1),


`y=x \\ \\ \Rightarrow x^2-3x=0 \\ \\ \Rightarrow x(x-3)=0 \\ \\ \Rightarrow x=0\ and\ x-3=0 \\ \\ \Rightarrow x=0\ and\ x=3`

Therefore, the local extremas are (0, 0) and (3, 3)