Question

F(x)=(x+3)^2-1

g(x)=-2x^2+8x+3
What are the x- and y- intercepts of the graph of the function f(x)? Identify the coordinates of any maxima or minima of the function. Explain your answers.

Answer 1

x-intercepts of f(x) are

`f(x)=(x+3)^(2)-1=0`

`x_(1)= -2, x_(2)=-4`
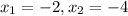
As points they are (-2,0) and (-4,0)
y-intercept of f(x) is

`f(0)=(0+3)^(2)-1=8`
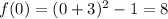
As a point it is (0,8)

x-intercepts of g(x) are:

`g(x)=-2 x^(2) +8x+3=0`

`x_(1)= (-4+ √(22) )/(-2) , x_(2)= (-4- √(22) )/(-2)`
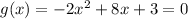
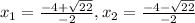
y-intercept of g(x) is:

`g(0)=-2*0+8*0+3=3`
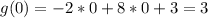
As a point it is (0,3)

f(x) has a minima, the function is cap-sized. Since we have a simple case of quadratic function, there is no need to check the second order derivative. Indeed, I will attach both graphs for f(x) and g(x). The minima of f(x) is (-3,-1). And g(x) has a maxima. This maxima is the point (2,11)