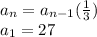Question

What is the recursive rule for this geometric sequence? 27,  9,  3,  1,  ... Enter your answers in the boxes.

an= ⋅an−1
a1=

Answer 1

`a_n=a_(n-1)((1)/(3))\\a_1=27`

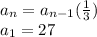
Explanation:

A recursive formula is a formula in which each term is based on the previous term.

In a geometric sequence, each term is found by multiplying the previous term by a constant.

To get from 27 to 9, then from 9 to 3, etc., we would multiply by 1/3. This makes the common ratio 1/3.

The recursive formula for a geometric sequence is

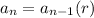`a_n=a_(n-1)(r)`, where
`a_n` represents the general term,
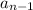`a_(n-1)`, represents the previous term, and r represents the common ratio.

Plugging in our values, we have

`a_n=a_(n-1)(r)`

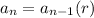
We also have to indicate what the first term, a₁, is. In this sequence, it is 21. This gives us

`a_n=a_(n-1)((1)/(3))\\a_1=27`