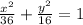Question

What is an equation in standard form of an ellipse centered at the origin with vertex (-6,0) and co-vertex (0,4)?

Answer 1

`(x^(2) )/(36)` +
`( y^(2))/(16)` = 1

This is because the standard form of an ellipse is


`( x^(2) )/( a^(2) )` +
`( y^(2) )/( b^(2) )` = 1

where a is the vertex and b is the co-vertex. So when we stick their respective x and y values in and then square them, you're left with the answer above.

Answer 2

`(x^(2) )/(36)+(y^(2) )/(16)=1`

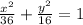
Explanation:

As we know standard equation of n ellipse is
`((x-0)^(2) )/((-6)^(2))+((y-0)^(2) )/((4)^(2) )=1`

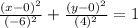
In the given equation (h, k) is the center, a is the vertex and b is the co-vertex.

Here vertex is (-6, 0) and co-vertex is (0, 4)

Therefore, length of a = -6, b = 4 and origin is (0, 0)

Now the equation of the ellipse will be

`((x-0)^(2) )/((-6)^(2))+((y-0)^(2) )/((4)^(2) )=1`

`(x^(2) )/(6^(2))+(y^(2) )/(4^(2) )=1`

`(x^(2) )/(36)+(y^(2) )/(16)=1`

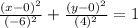
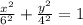
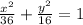
Therefore, the equation of the ellipse will be
`(x^(2) )/(36)+(y^(2) )/(16)=1`