To find the maximum number of mosquitoes, we are going to find the y-coordinate of vertex of our function, but we are going to expand our function:
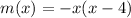

Now to find the vertex
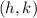
of our quadratic, we are going to use the vertex formula. For a quadratic function of the form
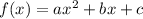
, its vertex
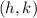
is given by the formula

and
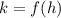
.
We can infer from our function that

and

, so lets replace those values in our formula:

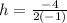
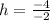
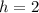
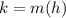
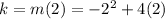
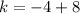
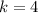
The vertex
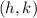
of our function is

, so the y-coordinate of the vertex is 4.
Since the y-coordinate of the vertex is the maximum number of mosquitoes, we can conclude that
he maximum possible number of mosquitoes is 4.