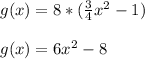Question # 1.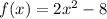
g(x) is the translation of f(x) 2 units down.
Vertical translation can be expressed as addition or subtraction of a number from the function value. Subtraction indicates that the function is translated down. So, translation of f(x) by 2 units down can be expressed as:
g(x) = f(x) - 2
Using the value of f(x), we can write:
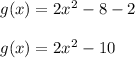 Question # 2
Question # 2
A function can be vertically stretched by multiplying it with a number having magnitude greater than 1. f(x) is to be stretched by a factor of 8 to get g(x), so we can write:
g(x) = 8 * f(x)
Using the value of f(x) we can write: