Question

1/4x+3=x+9

what value of x makes the statement true?

Answer 1

First, you would want to get x on one side of the equation. It is important to remember that what you do to one side of the equation, you must do to the other side. Let's rewrite the equation:


`(1)/(4)x +3=x+9`

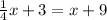
We know that we can also rewrite the equation to say:


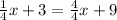
`(1)/(4)x+3= (4)/(4)x+9`, because
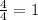
`(4)/(4)=1`, and we are not essentially changing the equation.

Let us subtract
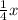
`(1)/(4)x` from both the left and right sides. We then get:


`3= (3)/(4)x+9`

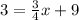
Now we want to isolate x on the right side, so we need to subtract 9 from both the right and left sides. So we get:


`-6= (3)/(4)x`

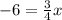
So now, when we solve for x, in order to get rid of this fraction that it is being multiplied by, let us multiply by the reciprocal (flipping the fraction). However it is important to keep in mind, that we do this to both sides. Let's see that:


`(4)/(3)(-6)= ((3)/(4)x)( (4)/(3))`

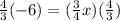
So now the right side cancels out, and we are left to solve the left side for x:


`(4)/(3)* (-6)/(1)=- (24)/(3)=-8`

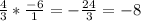
So now that we have solved the equation, we know that x = -8.

Answer 2

The correct answer is x=-8