To solve this we are going to use the formula for a rectangular prism:
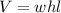
where
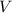
is the volume
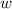
is the width

is the height
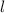
is the length
We know from our problem that our semitrailer has inner dimensions 2 meters wide by 10 meters long by 3 meters high, so
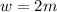
,
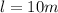
, and
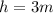
. Lets replace those values in our formula to find
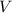
:
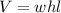
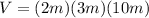

Now to find how many pallets we could load in the semitrailer, we just need to divide the volume of the volume of the semitrailer by the volume of one pallet:
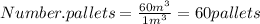
We can conclude that we could load
60 pallets in the semitrailer.