Lets rewrite the summation:
Summation from 1 to 12 of (2n+1) is equal to the summation of 1 to 12 of (2n) plus the summation from 1 to 12 of (1).
The summation from 1 to any number (

) is given by:
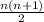
So, the first term of our rewritten summation is equal to
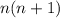
.
The summation from 1 to any number (

) of a constant (lets call it

) is given by:
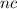
So, the whole summation can be written as:
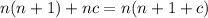
For your problem we have

and
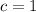
.
So, the answer is 168.