Answer:
63.39 yards.
Explanation:
Refer the attached figure
We are given that Caleb and Emily are standing 100 yards from each other i.e. BC = 100
Let BD = x
So, DC = 100-x
We are given that Caleb looks up at a 45° angle to see a hot air balloon i.e. ∠ABD = 45° and Emily looks up at a 60° angle to see the same hot air balloon i.e. ∠ACD = 60°
Let AD be the height of the balloon denoted by h.
In ΔABD
Using trigonometric ratio
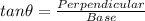

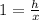
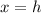 ---1
---1
In ΔACD
Using trigonometric ratio
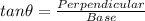
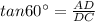
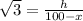
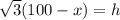 ---2
---2
So, equating 1 and 2
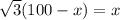
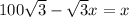
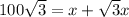

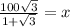
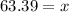
Thus the height of the balloon is 63.39 yards.