Answer:
The correct option is 4.
Explanation:
In triangle ABC and XYC,
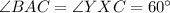 (Given)
(Given)
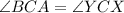 (Reflexive Property)
(Reflexive Property)
By AA rule of similarity,
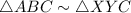
The corresponding sides of similar triangles are proportional.
Since triangle ABC and XYC, therefore
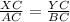
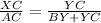
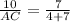
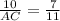
Therefore option 4 is correct.