Question

What is the vertex of the graph of the function below? y = x2 + 6x + 5

Answer 1

The vertex of the graph is (-3, -4).

Explanation:

Given quadratic function is,

`y=x^2+6x+5`

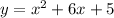
For finding the vertex we need to change the given expression in the form of
`y=a(x-h)^2+k`,

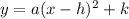For this we must add and subtract the square of the coefficient of middle term,

Since, the half of 6 = 3

Add and subtract the square of 3 in the right side of the equation,

`y=x^2+6x+5+9-9`

`y=(x^2+6x+9)+5-9`

`y=(x+3)^2-4`

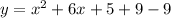
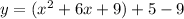
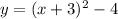
We know that,

For the function
`y=a(x-h)^2+k`

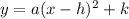
Vertex = (h,k)

By comparing,

The vertex of the given function is (-3, -4).

Answer 2

y = x² + 6x + 5
a=1, b+6, c=5
Axis of Symmetry: x = -b/2a
= -(6)/2(1)
= -3

Vertex: f(-3) = (-3)² + 6(-3) + 5
= 9 + -18 +5
= -4

(-3. -4)