Question

How can you use transformations to graph this function?

y= 3•7^-x+2

Explain your steps.

Answer 1

Sketch the graph of y= 7^x

Reflect the graph across the y-axis to show the function y= 7^-x

Stretch the graph vertically by a factor of 3 to show the function y= 3⋅7^-x

Shift the graph up 2 units to show the function y= 3 ⋅ 7^-x +2

Answer 2

The parent function for this function is


`f(x)= 7^(x)`

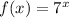
We have to explain how the given function can be obtained from the parent function.

Let y=g(x)

So,


`g(x)=3*7^(-x) +2`

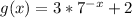
Notice that x in the exponent is multiplied by -1. Multiplying x by -1 implies the reflection of the graph across y-axis.

The function value is multiplied by 3. This suggest a vertical expansion by a factor of 3.

2 is being added to the function value, this implies a vertical shift upwards by 2 units.

So, we can write:

y = g(x) = 3f(-x) + 2

Thus following translations are applied:

a) Reflection across y-axis
b) Vertical stretch by a factor of 3
c) Upward shift by 2 units