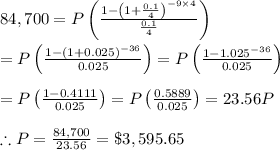Question

Find the amount of each payment necessary to amortize the following loan. A company borrows $84,700 for new equipment. The company agrees to make quarterly payments for 9 years at 10% per year. Find the amount of the quarterly payment.

Answer 1

This problem can be approached using the present value of annuity formula.

The present value of annuity is given by:


`PV=P \left((1-\left(1+(r)/(t)\right)^(-nt))/((r)/(t)) \right)`

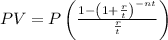
Where:: P is equal periodic payment, r is the annual interest rate, t is the number of payments in a year and n is the number of years for the loan to be paid.

Given that a company borrows $84,700 for new equipment and that the company agrees to make quarterly payments for 9 years at 10% per year.

Thus, P = $84,700; n = 9 years and r = 10% = 0.1.

Since the payment is to be made quarterly, thus, in one year, there will be 4 payments. i.e. t = 4.

Thus, we have:


`84,700=P \left((1-\left(1+(0.1)/(4)\right)^(-9*4))/((0.1)/(4)) \right) \\ \\ =P\left( (1-(1+0.025)^(-36))/(0.025) \right)=P\left((1-1.025^(-36))/(0.025)\right) \\ \\ =P\left((1-0.4111)/(0.025)\right)=P\left((0.5889)/(0.025)\right)=23.56P \\ \\ \therefore P= (84,700)/(23.56) =\$3,595.65`