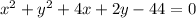Answer:
The equation of the given circle in general form is given by:
Option: A
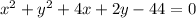
Explanation:
We know that the general equation of a circle with center at (h,k) and radius 'r' is given by:
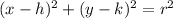
Clearly from the figure we have:
The center of the circle is at (-2,-1) and radius is 7 units.
i.e. we have: (h,k)=(-2,-1) and r=7
Hence, the equation of the circle is given by:

on expanding the terms we have:

Hence, the general equation of the circle is: