Not sure what "factor theorem" refers to, but one theorem it might be another name for could be the polynomial remainder theorem. It says that a polynomial
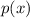
, when divided by a linear binomial

, leaves a remainder whose value is
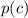
. If the remainder is 0, then

is a factor of
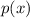
.
In this case, for
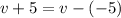
to be a factor of
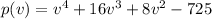
, we need to check
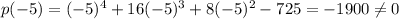
So
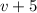
is not a factor of

.