Answer:
a) 128 b) 512
Explanation:
The key to solve this, is to think of it as a Geometric Sequence. Since, there is a constant ratio (q), each time the sheet of paper is cut, it is divided into two pieces or 1/2.
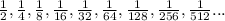
If after the 1st cut there are two pieces i.e. 1/2
a) After the 7th cut, how many of the smallest pieces of paper are there?
You can either count the sequence above: 1/128 then 128 pieces or apply the recursive formula for any Term of a Geometric Sequence;
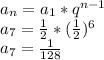
The Denominator indicates the smallest pieces of paper: 128
b) After the 9th cut, how many of the smallest pieces of paper are there?
Similarly to the item a: 1/512 then 512
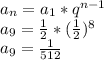
The Denominator indicates the smallest pieces of paper after the Ninth cut: 512