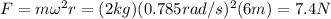The length of one revolution is equal to the perimeter of the orbit. Since the radius is r=6 m, the perimeter is
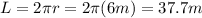
The object completes one revolution every 8 seconds, so its frequency of revolution is

and the angular frequency is
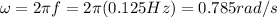
So now we can find the centripetal force acting on the body, which is equal to