Question

Please help Find x
​

Answer 1

Answer: x = 12

====================================================

Step-by-step explanation:

The hexagon is broken up into 6 congruent or identical equilateral triangles. If we find the area of one triangle, then we multiply by 6 to get the area of the hexagon.

Going in reverse, we divide the hexagon's area by 6 to get the area of one equilateral triangle

We're told the hexagon has an area of
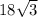`18√(3)` square inches. Divide this by 6 and you should get the result
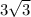`3√(3)`. So each of the six equilateral triangles has area of
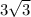`3√(3)` square inches.

-------------------------------------

Each triangle has a base of
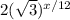`2(√(3))^(x/12)` and a height of
`(√(3))^(x/6)`

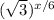
The x/12 and x/6 are exponents.

Let
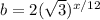`b = 2(√(3))^(x/12)` and
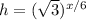`h = (√(3))^(x/6)` be the base and height respectively.

Also, let
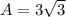`A = 3√(3)` be the area of the triangle

We can then solve for x like so:

`A = 0.5*b*h\\\\3√(3) = 0.5*2(√(3))^(x/12)*(√(3))^(x/6)\\\\3*3^(1/2) = (√(3))^(x/12+x/6)\\\\3^1*3^(1/2) = (√(3))^(x/12+2x/12)\\\\3^(1+1/2) = (√(3))^(3x/12)\\\\3^(3/2) = (3^(1/2))^(x/4)\\\\3^(3/2) = 3^((1/2)*(x/4))\\\\3^(3/2) = 3^(x/8)\\\\`

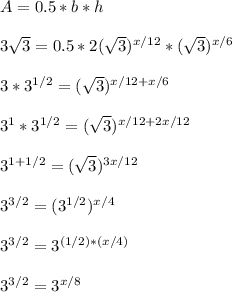
Since the bases are equal to 3, this means the exponents must be equal as well (for both sides overall to be equal)

3/2 = x/8

3*8 = 2*x ... cross multiply

24 = 2x

2x = 24

x = 24/2

x = 12