Question

Jerry starts to save at age 35 for a vacation home that he wants to buy for his 50th birthday. He will contribute $300 each month to an account, which earns 1.7% interest, compounded annually. What is the future value of this investment, rounded to the nearest dollar, when Jerry is ready to purchase the vacation home? Answers: $61,960 $60,924 $5,077 $5,163 . Please help. I would also appreciate if someone had the formula for this, i think i have it wrong

Answer 1

If Jerry contributes at the beginning of the month and withdraws at the end of the month, the final contribution earns 1 month's interest. The one before that earns 2 months' interest, so has a value of (1+0.017/12) times that of the last payment. In short, the sum is that of a geometric sequence with first term
a₁ = 300*(1+0.017/12)
and common ratio
r = 1+0.017/12

We assume Jerry contributes each month for 15 years, so a total of 180 payments. The sum is given by the formula for the sum of a geometric sequence.

`S_(n)=a_(1)\cdot (r^(n)-1)/(r-1)`
Filling in your numbers, this is

`S_(180)=300(1+(0.017)/(12))\left( ((1+(0.017)/(12))^(180))/(((0.017)/(12))) \right) \approx 61547`

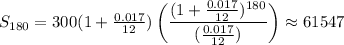
If Jerry's contributions and withdrawal are at the end of the month, this balance is reduced by 1 month's interest, so is $61,460.

_____
We suppose the expected choice is $61,960. This supposition comes from the fact that a handwritten 4 is often confused with a handwritten 9. The usual simple calculation of future value uses end-of-the-month contributions by default. (a₁ = 300)