Answer:
81
Explanation:
The relevant rules of exponents are ...
(ab)^c = (a^c)(b^c)
a^-b = 1/a^b
(a^b)(a^c) = a^(b+c)
(a^b)^c = a^(bc)
__
Applying these rules, we can simplify this expression as follows:
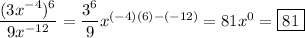
_____
Additional comment
The rules of exponents derive from the fact that an exponent indicates repeated multiplication. That is, x·x·x = x³, where the exponent 3 indicates x is a factor 3 times. When this idea is used for division, we see the exponent is the difference between numerator and denominator exponents:
(x·x·x)/(x·x) = x or x³/x² = x³⁻² = x¹ = x
This idea extends to cases where the denominator exponent is larger:
(x·x)/(x·x·x) = 1/x or x²/x³ = x²⁻³ = x⁻¹ = 1/x
This can help you see that moving a factor from numerator to denominator (or vice versa) changes the sign of its exponent.
__
This idea of repeated multiplication also applies when exponents are layered:
(x·x·x)(x·x·x) = (x³)² = x⁶ . . . . . the product exponent is the product of 3 and 2 as we indicated in the rules above