Question

Which of the following numbers is irrational? a fraction with numerator negative 15 and denominator 4, a fraction with numerator negative 7 and denominator 9, square root of 4, π a fraction with numerator negative 15 and denominator 4 a fraction with numerator negative 7 and denominator 9 square root of 4 π

Answer 1

Pi is an irrational number

Answer 2

π is irrational.

Explanation:

Since, a real number is called rational if it can be expressed as
`(p)/(q)`,

Where,

p and q are integers,

Such that, q ≠ 0,

Otherwise, the real number is called irrational.

Since, -15, 4, -7, 9 are integers,

Such that, 4, 9 ≠ 0

Thus,

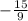`-(15)/(9)` and
`(-7)/(9)` are rational numbers ⇒ they are not irrational,

Now,

√4 = 2 =
`(2)/(1)`

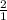
Where, 2 and 1 are integers such that 1 ≠ 0,

Thus, √4 is not irrational,

While,

π = 3.14159265359....

Which is a non terminating non recurring decimal,

That is, it can not be expressed as
`(p)/(q)` where, p and q are integers such that q ≠ 0

Hence, π is irrational.