Answer:
The correct option is 4. The vertex of the parabola is (10,800).
Explanation:
If a quadratic function is defined as
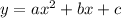
then its vertex is
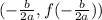
The given quadratic function is
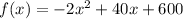
Here, a=-2, b=40 c=400.
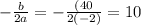
Substitute x=10 in the given function.
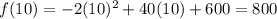
The vertex of the given function is (10,800). Therefore correct option is 4.