Question

Evaluate the following expression log3 9

Answer 1

`\bf \textit{Logarithm Cancellation Rules} \\\\ \boxed{log_a a^x = x}\qquad \qquad a^(log_a x)=x\\\\ -------------------------------\\\\ log_3(9)\qquad \qquad \underline{9=3^2}\qquad \qquad log_3(\underline{3^2})\implies 2`

Answer 2

Answer: The solution for the given expression is 2.

Explanation:

We are given:

An expression having value:
`\log_3 9`

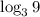
Using the identities:

`\log_a x^n=n\log_a x` ......(1)

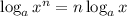`\log_a a=1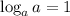` ......(2)

Evaluating the expression:

`\Rightarrow \log_3 9=\log _3 3^2`

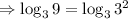
Using identity 1:

`\Rightarrow \log _3 3^2=2\log_3 3`

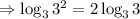
Using identity 2:

`2\log_3 3=2* 1=2`

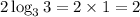
Hence, the solution for the given expression is 2.