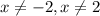Question

Which domain restrictions apply to the rational expression? x^2+4x+4 / x^2−4 Select each correct answer x≠−4 x≠−2 x≠0 x≠2 x≠4

Answer 1

The restrictions on domain are are:
`x \\eq -2, x\\eq 2`

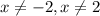
Explanation:

We are given the following information in the question:

We are given an expression:

`\displaystyle(x^2 + 4x +4)/(x^2-4)`

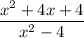
Simplifying the given fraction, we have,

`\displaystyle(x^2 + 4x +4)/(x^2-4)\\\\=((x+2)^2)/((x+2)(x-2))\\\\=((x+2)(x+2))/((x+2)(x-2))`

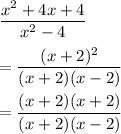
The domain is basically collection of all values of x such that the expression is defined.

We need to make sure that the denominator is not equal to zero for the given fraction.

Thus,

`(x+2)(x-2) \\eq 0\\\Rightarrow (x+2) \\eq 0, (x-2) \\eq 0\\\Rightarrow x \\eq -2, x\\eq 2`

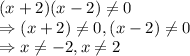
Hence, the restrictions on domain are are:

`x \\eq -2, x\\eq 2`

Answer 2

The correct answers are x≠2 and x≠(-2).

Domain restrictions are any points in the domain where the function will not have a value. This basically means that it's a point where x won't work in the function.

For the numerator, any value will work for x. We can have a value of 0 in the numerator, or a positive, negative, or decimal number.

However, the denominator cannot equal 0. This is because a fraction bar represents division, and we cannot divide by 0. The values that make the denominator 0 can be found by:

x²-4=0

Add 4 to both sides:
x²-4+4 = 0+4
x² = 4

Take the square root of both sides:
√x² = √4

x = 2 or x = -2.