Question

Question:

Greg and Anna drive uphill from Lakeshore to Valley View Point, and back downhill to Lakeshore. They notice that the drive uphill takes 10 minutes less than twice the time to drive downhill. The difference between the time taken to drive uphill and the time to drive downhill is 65 minutes.

Write a pair of linear equations to represent the information given above. Be sure to state what the variables represent.
Explain how you can change this pair of equations to one linear equation in one variable.
Apply your method to find how long the drive uphill takes. Show your work.

Type your answer below:
Edit View Format Table

Formats

Answer 1

Let's denote x to be the time needed to drive uphill and y-the time needed to drive downhill, then 2y is a double time to drive downhill. The first condition says that 2y-x=10. The difference between driving uphill and downhill is 65 minutes, so x-y=65. Therefore, we obtain two equations, which we combine into the system
`\left \{ {{2y-x=10} \atop {x-y=65}} \right.`.

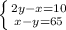To solve this system let's express x= 65+y and then 2y-(65+y)=10, which implies y=75 minutes and x=65+75=140 minutes. The drive uphill takes 140 minutes and the drive downhill takes 75 minutes.

If we denote x to be the time needed to drive uphill, then the time needed to drive downhill will be x-65 and double time to drive downhill will be 2(x-65)=2x-130. The difference between times is 10 minutes, thus 2x-130-x=10, from where we have x=140 and x-65=140-65=75.