Question

Consider the system below. 4x-2y=-12 3x-y=-3 Solve the system by using a matrix equation. Show your work.

Answer 1

The matrix equation AX=B, where A and B are numerical matrices and X is unknown matrix has a solution
`X= A^(-1) B`, where
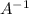
`A^(-1)` is inverse matrix of X.
1. We rewrite given system as matrix equation
`\left[\begin{array}{cc}4&-2\\3&-1\end{array}\right] X=\left[\begin{array}{c}- 12\\- 3\end{array}\right]`;
2. Find
`A^(-1) = \left[\begin{array}{cc}4&-2\\3&-1\end{array}\right] ^(-1)` by the rule
`A^(-1)= (1)/(det \ A) [ A_(ij) ] ^(T)`. So,
`det\ A=4`×
`(-1)-3`×
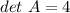
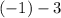
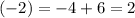
`(-2)=-4+6=2` and algebraic supplements are

`A_(11) =-1 \\ A_(12) =-3 \\ A_(21)=2 \\ A_(22) =4`. Then
`A^(-1) = (1)/(2) \left[\begin{array}{cc}-1&-3\\2&4\end{array}\right] ^(T)= \left[\begin{array}{cc}- (1)/(2) &1\\- (3)/(2) &2\end{array}\right]`;
3. Calculate
`X= \left[\begin{array}{cc}- (1)/(2) &1\\- (3)/(2) &2\end{array}\right] \left[\begin{array}{c} -12\\-3\end{array}\right]=`
`\left[\begin{array}{c}3\\12\end{array}\right]`;

4. We obtain
`X= \left[\begin{array}{c}3\\12\end{array}\right]`, from where x=3 and y=12.