Question

A triangle has side lengths 4, 7 and 9. What is the measure of the angle across from the longest side?

92 = 42 + 72 − 2g4g7cos(A)
81 = 16 + 49 − 56cos(A)
81 = 9cos(A)
9 = cos(A)
A cannot exist!

Gabe tried to use the law of cosines to find an unknown angle measure in a triangle. His work is shown. What is Gabe’s error?

Gabe reversed the order of the 9 and the 4.

Gabe squared the numbers incorrectly.

Gabe should not have subtracted 56 from
16 + 49.

Gabe incorrectly stated that cos–1(9) is not defined.

Answer 1

Explanation:

Given that a triangle has sides 4,7 and 9

A student Gabe tried to use law of cosines to find unknown angle measure

The angle is opposite side 9 because angle across the longest side is given

He used cosine formula for triangles

`a^2=b^2+c^2-2bccosA\\9^2 = 4^2+7^2-2(4)(8) cosA\\81-65 =-56 cosA\\`

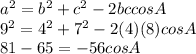
But instead he adjusted -56 with 16 +49 which is wrong

Because -56 has product as cosA it is not like term as other constants

So correct step should be

81 = 65-56 Cos A

Gabe should not have subtracted 56 from

16 + 49.

This is the correct answer

Answer 2

The third choice is the best:
Gabe should not have subtracted 56 from 16+49.

_____
Rather, Gabe should have subtracted 16+49 from 81 to get
16 = -56cos(A)
cos(A) = -16/56 = -2/7
A = arccos(-2/7) ≈ 106.6°