Question

Determine

a) the electric field strength at a point x at a distance 20cm from a point charge Q= +6uc
b) the electric force that acts on a point charge q=-0.20uc placed at point x.

Answer 1

a) The magnitude of the electric field generated by a point charge Q at distance r from the charge is

`E=k (Q)/(r^2)`
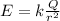
where k is the Coulomb's constant. In this problem, the charge is

`Q=6 \mu C=6 \cdot 10^(-6) C`
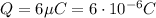
and the distance is

`r=20 cm=0.20 m`
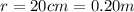
Therefore the electric field is

`E=k (Q)/(r^2)=(8.99 \cdot 10^9 Nm^2C^(-2)) (6 \cdot 10^(-6) C)/((0.20 m)^2)=1.36 \cdot 10^6 N/C`

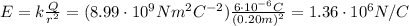
b) The electric force acting on a charge q is given by

`F=qE`
where E is the intensity of the electric field at the point where the charge q is located.
We have already calculated the magnitude of the electric field, E, at point x, therefore the force acting on the charge is

`F=qE=(-0.20 \cdot 10^(-6) C)(1.36 \cdot 10^6 N/C)=-0.272 N`
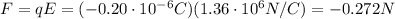
and the negative sign means the force points in the opposite direction of the electric field, since the charge is negative.