50 pounds of cashews and 71 pounds of walnuts were sold.
Our system of equations is
p+n = 121
p+4.19n = 280.50
Since the coefficients of p are the same, we will begin solving this by subtracting the second equation from the first:
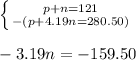
Divide both sides by -3.19:
-3.19n/-3.19 = -159.50/-3.19
n = 50
There were 50 pounds of cashews sold.
To find the value of p, the pounds of walnuts, substitute 50 in for n in the first equation:
p+n = 121
p+50 = 121
Subtract 50 from both sides:
p+50-50 = 121-50
p=71
71 pounds of walnuts were sold.