Question

Please helpppp it has to do with P(A U B)

Answer 1

`P(A)=0.5`,
`P(B)=0.6`,
`P(A\cup B)=0.8`

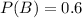
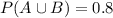
We find the probability of intersection using the inclusion/exclusion principle:



`P(A\cap B)=P(A)+P(B)-P(A\cup B)=0.3`


By definition of conditional probability,



`P(A\mid B)=(P(A\cap B))/(P(B))=(0.3)/(0.6)=0.5`


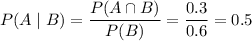
For
`A` and
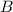
`B` to be independent, we must have



`P(A\cap B)=P(A)\cdot P(B)`

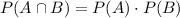
in which case we have
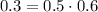
`0.3=0.5\cdot0.6`, which is true, so
`A` and
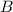
`B` are indeed independent.


Or, to establish independence another way, in terms of conditional probability, we must have


`P(A\mid B)\cdot P(B)=P(A)\cdot P(B)\implies P(A\mid B)=P(A)`


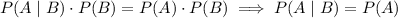
which is also true.