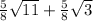Question

What is the following quotient? 5/√11-√3

Answer 1

B

Explanation:

Answer 2

`\frac{5( √(11) + √(3) )} {8}`

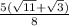
EXPLANATION

The given rational function is

`(5)/( √(11) - √(3))`

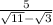
We need to rationalize the denominator by multiplying both the numerator and the denominator by the conjugate of

`√(11) - √(3)`

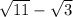
which is

`√(11) + √(3)`

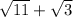
When we rationalize we obtain:

`(5( √(11) + √(3) ))/((√(11) - √(3) )( √(11) + √(3) ))`

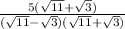
The denominator is now a difference of two squares:

`(a - b)(a + b) = {a}^(2) - {b}^(2)`

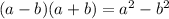
We apply this property to get

`(5( √(11) + √(3) ))/(( √(11)) ^(2) - ( √(3)) ^(2) ))`

`(5( √(11) + √(3) ))/(11 - 3)`

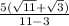
This simplifies to

`\frac{5( √(11) + √(3) )} {8}`

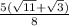
Or

`\frac{5 } {8}√(11) + \frac{5 } {8}√(3)`