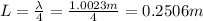Question

Pipin' pete is playing at city park next weekend. one of the closed-end pipes is capable of sounding out a first harmonic of 349.2 hz. the speed of sound in the pipe is 350 m/sec. find the length of the air column inside the pipe. give your answer in meters.

Answer 1

The frequency of the first harmonic in the pipe is

`f = 349.2 Hz`
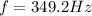
and the speed of sound in the pipe is

`v=350 m/s`
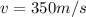
So the wavelength of the first harmonic in the pipe is

`\lambda= (v)/(f)= (350 m/s)/(349.2 Hz)=1.0023 m`

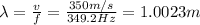
For a closed-end pipe, the wavelength of the first harmonic is four times the length of the pipe:

`\lambda=4 L`
Therefore, the length of the pipe is

`L= (\lambda)/(4)= (1.0023 m)/(4)=0.2506 m`