Question

In a binomial trail, the probability of success is 0.6 for each trial. Find the probability of each of the following.

51. 9 success in 20 trials
53. 6 failures in 12 trials
And could you show your work plz

Answer 1

Answer with Step-by-step explanation:

The formula for finding the probability of r success in binomial trail is:

P(r success) =
`(n!)/((n-r)!r!)p^rq^(n-r)`

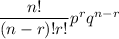
where n is the number of trials,p is the probability of success and q is the probability of failure.

q=1-p

Here, p=0.6

⇒q=1-0.6

⇒q=0.4

9 success in 20 trials

r=9 and n=20

P(9 success)=
`(20!)/((20-9)!9!)0.6^90.4^(20-9)`

=
`(20!)/(11!9!)0.6^90.4^(11)`

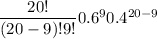
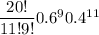
= 0.07

6 failures in 12 trials

P(6 failures)=P(12-6 success)

=P(6 success)

=
`(12!)/((12-6)!6!)0.6^60.4^(12-6)`

=
`(12!)/(6!6!)0.6^60.4^6`

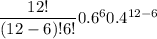
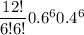
= 0.18

Answer 2

Binomial distribution is given by the formula:
p(x=r)=(n!/(r!(n-r)!))p^r q^(n-r)
thus:
a] Probability of obtaining 9 success in 20 trials will be:
P(x)=[20!/(9!(20-9)!)]*0.6^9*0.4^(20-9)
Simplifying the above we get:
P(x)=167960*0.6^9*0.4^11
P(x)=0.071

b] Probability of obtaining 6 failures in 12 trials
P(x)=[12!/(6!(12-6)!)]*0.4^6*(0.6)^(12-6)
simplifying the above we obtain:
P(x)=924*0.4^6*0.6^6
P(x)=0.1766