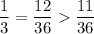Two numbers are drawn without replacement. The only way their product is zero is if one of these numbers is zero. The probability of this happening is
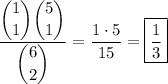
In other words,
• there is 1 zero in the list - we draw it with
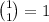 way of doing so;
way of doing so;
• there are 5 non-zero numbers in the list - we draw 1 of these, with
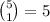 ways of doing so;
ways of doing so;
• there is a total of 6 numbers in the list - we draw 2 of these, with
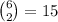 ways of doing so.
ways of doing so.
On the other hand, if the numbers are drawn with replacement and independently of one another, then each number has the same probability of getting drawn each time. There are 6×6 = 36 possible outcomes, each with 1/36 probability of occurring. Their product is zero if at least one of the numbers drawn is zero. The probability of this happening is
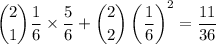
That is,
• there is 1/6 chance of drawing a zero and 5/6 chance of not drawing a zero. This can selection can happen in
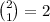 ways (zero is drawn first or last);
ways (zero is drawn first or last);
• there is 1/6 chance of drawing a zero for either selection. This can happen in
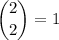 way (zero is drawn both times).
way (zero is drawn both times).
While the probabilities are close, they are not the same! Be careful with which interpretation you choose.