Question

The function h(x) = 1/2 (x+3)2 +2. How is the graph of the h(x) translated from the parent graph of a quadratic function, F(x) =x2 Select all that apply

Answer 1

For this case, the parent function is given by:

`F (x) = x ^ 2`
We apply the following function transformation:
Vertical compressions:
To graph y = a * f (x)
If 0 <a <1, the graph of y = f (x) is compressed vertically by a factor a. (Shrinks)
We have then:

`y = (1/2) * x ^ 2`
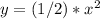
Horizontal translations:
Suppose that h> 0
To graph y = f (x + h), move the graph of h units to the left.
We have then:

`y = (1/2) * (x + 3) ^ 2`
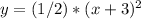
Vertical translations:
Suppose that k> 0
To graph y = f (x) + k, move the graph of k units up.
We have then:

`h (x) = (1/2) * (x + 3) ^ 2 + 2`
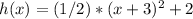Answer:
Vertical compression by factor of 1/2. Horizontal displacement 3 units to the left. Vertical displacement 2 units up.