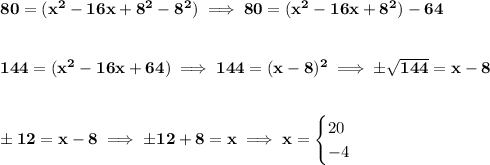Question

How do you solve basic quadratic equations, using the "completing the square" method. I know how to use the quadratic formula but don't know how to solve by completing the square.

Answer 1

so, we have 80 = x² -16x.

first off, we start by grouping the terms with "x".

80 = (x² - 16x)

80 = (x² - 16x + [?]²) <--- we have a missing fellow.

so, the idea being, we need "some value" to get our perfect square trinomial, hmmm what could that be?

well, the tell-tale guy is the middle term, we know that 2(√ guy on the left)(√ guy on the right) is the middle term.

we know the square root of the (√x²) is just "x", and the guy on the right is [?], but we also know that if we multiply 2 times both we get 16x, so


`\bf 2(x)\left(\boxed{?}\right)=16x\implies \boxed{?}=\cfrac{16x}{2x}\implies \boxed{?}=8`

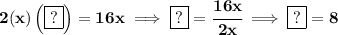
aha! there's our missing fellow, so we need to add 8².

however, bear in mind, all we're doing is borrowing from our very good friend Mr Zero, 0.

so if we add 8², we also have to subtract 8².


`\bf 80=(x^2-16x+8^2-8^2)\implies 80=(x^2-16x+8^2)-64 \\\\\\ 144=(x^2-16x+64)\implies 144=(x-8)^2\implies \pm√(144)=x-8 \\\\\\ \pm 12 = x-8\implies \pm 12 + 8 = x\implies x= \begin{cases} 20\\ -4 \end{cases}`