Question

HELP FAST PLEASE? In △XYZ , m∠X=38∘ , m∠Z=67∘ , and YZ=25 feet . What is XZ ? Enter your answer as a decimal in the box. Round only your final answer to the nearest tenth. ft

Answer 1

x = 33.49 degrees because sin x = 32/58 so divide 32/58 and then press the sin^-1 and you get x = 33.49 degrees

Answer 2

Given △XYZ , m∠X=38∘ , m∠Z=67∘ , and YZ=25 feet . we need to find XZ.

Two angles and one side is given to us.

In any triangle sum of angles =180°

In triangle XYZ,<X+<Y+<Z=180°

Or 38+<Y+67 = 180

< Y+105= 180°

<Y = 75°

We can apply sine rule to find XZ

The sine Rule states in any triangle ABC ,

`(Sin A)/(a) =(Sin B)/(b) =(SinC)/(c)`

Applying the rule to triangle XYZ to find XZ we have:

`(Sin 38)/(25) =(Sin 75 )/(XZ)`

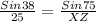
Cross multiplying we have:

XZ .Sin 38= 25 .Sin75

Substituting Sin38 and Sin 75 values we have:

XZ(0.62)= 25(0.97)

0.62 XZ= 24.15

XZ= 38.94 feet.