Question

Given the figure below, find the values of x and z.

Answer 1

x = 14° and z = 83°

Explanation:

We know that the vertical angles of intersecting lines are equal.

Thus, 13x - 85 = 97

i.e. 13x = 97 + 85

i.e. 13x = 182

i.e.
`x=(182)/(13)`

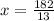
i.e. x = 14°

Since, the sum of all the four angles formed by intersecting line is 360°.

We get,

(13x-85) + 97 + 2z = 360° (Take 2z as opposite angles are equal)

i.e. 2z = 360 - 97 + 85 - 13 × 14

i.e. 2z = 360 - 12 - 182

i.e. 2z = 360 - 194

i.e. 2z = 166

i.e.
`z=(166)/(2)`

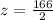
i.e. z = 83°

Hence, we get the angles x = 14° and z = 83°.

Answer 2

First, because 13x-85 and 97 are across from each other like that, you know that they are equal to each other. If you solve, you know that x is equal to 14. Then, you know that all the angles must equal 360 degrees. If you add 97 and 97 together, you get 194. Now, subtract that by 360, and you get the remaining degrees of the other two angles. Then, divide that by two, and z equals 83. Hope this helped!