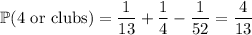Question

A card is drawn from a standard deck of cards. Determine whether the events are mutually exclusive or inclusive. Then, find the probability. P(a 4 or a club)

Answer 1

The events are not mutually exclusive because there is a 4 of clubs (both a 4 and of the club suit). So the probability we want would be


`\mathbb P(\text{4 or club})=\mathbb P(\text{4})+\mathbb P(\text{club})-\mathbb P(\text{4 and club})`

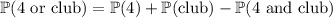
There are four 4's in the deck, so the probability of drawing a 4 is


`\mathbb P(\text{4})=\frac{\binom41\binom{48}0}{\binom{52}1}=\frac4{52}=\frac1{13}`

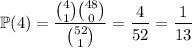
(I use the binomial coefficient here just to illustrate how we're counting the number of ways to draw a 4. There are four possible ways to draw one of them, i.e. 4 choose 1. On the other hand, we are not drawing any of the other 48 remaining cards, i.e. 48 choose 0. In the denominator, we're drawing 1 card from 52, i.e. 52 choose 1.)
There are 13 clubs in total, so the probability of drawing just 1 one of them is


`\mathbb P(\text{club})=\frac{\binom{13}1\binom{39}0}{\binom{52}1}=(13)/(52)=\frac14`

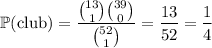
There is only one 4 of clubs in the deck. The probability of drawing it is


`\mathbb P(\text{4 and clubs})=\frac{\binom11\binom{51}0}{\binom{52}1}=\frac1{52}`

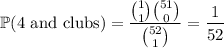
So the probability we care about is


`\mathbb P(\text{4 or clubs})=\frac1{13}+\frac14-\frac1{52}=\frac4{13}`

Answer 2

The events are not mutually exclusive

My explination is too long