Answer:
The measure of arc JH is 44°.
Explanation:
Given information: ∠JOH = 27° and arc NML = 98°.
If two chord intersect outside the circle, then
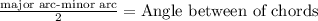
From the given figure it is clear that the major arc is NML and the minor arc is JH.
Let the measure of arc JH be x.
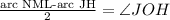
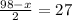
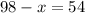
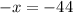
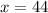
Therefore the measure of arc JH is 44°.