Question

Given: AG and CI are common internal tangents of H and B. HG = 7, ED = 7, and ED = EF.

What is the measure of EC?

Answer 1

EC = 24

This is because CBE is a right triangle with a right angle at angle ECB. Then we know that BC =7 and EB = 25. Use the Pythagorean Theorem to find EC.

Answer 2

EC = 12.12

Explanation:

Given H and B are circles of radius 7

ED = 7

CB = 7, so DB is also 7

Therefore, EB = ED + DB

= 7 + 7

= 14

Since IC is tangent at C we know that it is making a right angle to the radius CB.

Therefore, Triangle EBC is a right angle triangle where CB = 7 and EB = 14

Therefore from Pythagoras theorem,

`(EB)^(2)= (EC)^(2)+(CB)^(2)`

`(EC)^(2)= (EB)^(2)-(CB)^(2)`

`(EC)^(2)= (14)^(2)-(7)^(2)`

`(EC)^(2)= 196-49`

`(EC)^(2)= 147`

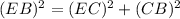
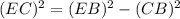
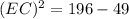
Therefore, EC = 12.12