Question

Solve the equation for x, where x is a real number (5 points):
-3x^2 + 4x - 31 = 23

Answer 1

Subtract 23 to both sides so that the equation becomes -3x^2 + 4x - 54 = 0.
To find the solutions to this equation, we can apply the quadratic formula. This quadratic formula solves equations of the form ax^2 + bx + c = 0
x = [ -b ± √(b^2 - 4ac) ] / (2a)
x = [ -4 ± √(4^2 - 4(-3)(-54)) ] / ( 2(-3) )
x = [ -4 ± √(16 - (648) ) ] / ( -6 )
x = [ -4 ± √(-632) ] / ( -6)
Since √-632 is nonreal, the answer to this question is that there are no real solutions.

Answer 2

Do you realize that you have given out 50 points?

Step One
Start by subtracting 23 from both sides.
-3x^2 + 4x - 31 -23 = 0
-3x^2 + 4x - 54 = 0

This does not give you a real result. We'll solve it anyway

Step two
bring out the quadratic equation and solve that
a = - 3
b = 4
c = -54


`\text{x = }\frac{ -b \pm \sqrt{b^(2) - 4ac } }{2a}`


`\text{x = }\frac{ -(4 ) \pm \sqrt{4^(2) - 4(-3)*(-54) } }{2(-3)}\\ \\\text{x = }( -(4) \pm √(16 - 648 ) )/(-6)\\ \\ \text{x = }( -(4) \pm √(-632 ) )/(-6)`

`\text{x = }( -(4) \pm √(4* -158 ) )/(-6)`

`\text{x = }( -(4) \pm 2√( -158 ) )/(-6)`

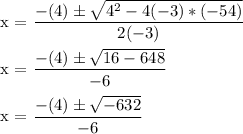
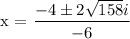`\text{x = }( -4 \pm 2√( 158 )i)/(-6)`x = 0.666 +/- 2 sqrt(158)i/ - 6x = 0.666 -/+ 4.1899ix1 = 0.666 - 4.1899ix2 = 0.666 + 4.1899i